Contenido:
Producto
Cartesiano
Definición
El producto
cartesiano de A y B, se define por
A × B = {(a,
b)/a ∈ A ∧ b ∈
B}
A y B conjuntos
dados, A × B se lee A cruz B
(a, b) es un
par ordenado, recuerde que a es el primer elemento del par y b es
el segundo, en
consecuencia (a, b) 6= (b, a)
Numero de
elementos
Sea m el número
de elementos de A (es decir su cardinalidad) y n el número
de elementos de
B, entonces mn es el número de elementos de los productos
A × B y B × A
Gráfico
Los pares
ordenados (3, 4) y (5, 2) están representados en el siguiente plano
cartesiano (gráfico):
Relaciones
Definición
R es una
relación de A en B si y solo si: R ⊆
A × B.
Así, notemos
que los elementos de una relación son pares ordenados.
Luis Zegarra
Relaciones y funciones 34
Notación
1. R es una
relación de A en B, también se denota por R : A → B
(x, y) ∈ R ∨
xRy ∨ y = R(x)
Representación gráfica de las relaciones
Los pares ordenados se pueden representar gráficamente por medio de diagramas sagitales o por medio de puntos en el plano cartesiano. Veamos el siguiente ejemplo.
Ejemplo 4
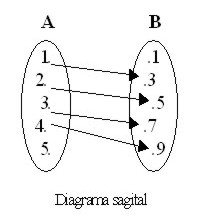
Si A = {1, 2, 3, 4, 5} y B = {1, 3, 5, 7, 9} y R la relación definida por la regla
R = {(x, y) / y = 2x + 1}, graficar R.
Solución
Los pares ordenados que pertenecen a la relación (que cumplen con y = 2x + 1) son:
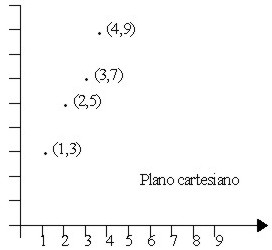
R = {(1, 3), (2, 5), (3, 7), (4, 9)}
Y la gráfica correspondiente es la siguiente:
Dominio
de una relación.
Sea R una
relación.
Definimos el
dominio de R como el conjunto formado por las primeras
componentes de las parejas ordenadas que pertenecen a R y lo
notamos D ( R ) o dom ( R ).
Dicho conjunto lo representamos por comprensión así:
D(R) = { x / ( Ǝ y ) ( ( x , y ) ϵ R ) }
Ejemplos:
de Dominio de Relación
Rango de una relación.
Sea R una relación
Definimos el rango de R como el conjunto formado por las segundas componentes de las parejas ordenadas que pertenecen a R y lo notamos r ( R ) o ran ( R ). Dicho conjunto lo representamos por comprensión así:
DI ( R ) = { y / ( Ǝx ) ( ( x , y ) ϵ R ) }
Relaciones de equivalencia
Las relaciones de equivalencia son relaciones entre los elementos de un conjunto cualquiera y su característica principal es que abstraen el concepto de igualdad.
La importancia de estas relaciones consiste en que dividen a los elementos del conjunto en diferentes clases, llamadas clases de equivalencia, de tal suerte que cada elemento pertenece a una y sólo una clase.
Tomemos un conjunto cualquiera X y sean a y b dos elementos en X (lo cual denotamos por a,b\in X). Si a está relacionado con b escribiremos a\sim b. Una relación de equivalencia en X es una relación que satisface las siguientes propiedades:
Sean A un conjunto y R una relación. Se dice que ■ R es reflexiva si : ∀x, ( x ∈ A → (x, x ) ∈ R ). Es decir, toda relación que sea reflexiva debe tener al menos n flechas (suponiendo que n es el número de elementos de A): deben estar todas las parejas (a, a ) donde a barre todos los elementos de A.
Ejemplo#1
Relación
Simétrica
Definición
Sean A un conjunto y R una relación. Se
dice que R es simétrica si ∀x,
y, ((x, y ) ∈ R → (y, x
) ∈ R ). Que
no nos engañe la implicación: no dice que tengamos flechas de x a y para todo x
y y: Dice que en caso de haber una flecha de x a y debemos de tener una de y a
x en las relaciones simétricas.
Propiedad simétrica
Relación
transitiva
Definición
Sean A un conjunto y R una relación. Se
dice que R es transitiva si ∀x,
y, z, ((x, y ) ∈ R ∧ (y, z ) ∈ R → (x, z ) ∈ R ).
Una relación es transitiva si cada vez
que un elemento está relacionado con otro, y éste está a su vez relacionado con
un tercero, el primer elemento está relacionado con el tercero.
Relación transitiva
Ejemplo#3
Relación inversa
Definición
Sea R : A → B una relación dada. Se define R−1 : B → A como: R −1 = {(x, y) ∈ B × A : (y, x) ∈ R} Nótese que Dom R−1 = Rec R y Rec R−1 = Dom R También que si: (x, y) ∈ (R−1 ) −1 ⇔ (y, x) ∈ R−1 ⇔ (x, y) ∈ R por tanto (R−1 ) −1 = R
COMPOSICIÓN DE RELACIONES
Sea
una relación de A en B y 
una relación de B en C. La composición de y es una relación consistente de los pares ordenados (a, c), donde a 
A y c C y para los cuales existe un b B tal que (a, b) y (b, c) , es decir a b y b c.
La composición se denota por
, si y son relaciones.
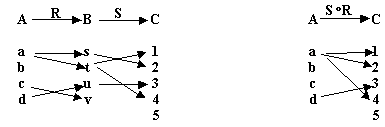
Sea R : A → B una relación dada. Se define R−1 : B → A como: R −1 = {(x, y) ∈ B × A : (y, x) ∈ R} Nótese que Dom R−1 = Rec R y Rec R−1 = Dom R También que si: (x, y) ∈ (R−1 ) −1 ⇔ (y, x) ∈ R−1 ⇔ (x, y) ∈ R por tanto (R−1 ) −1 = R
COMPOSICIÓN DE RELACIONES
Sea
una relación de A en B y una relación de B en C. La composición de y es una relación consistente de los pares ordenados (a, c), donde a A y c C y para los cuales existe un b B tal que (a, b) y (b, c) , es decir a b y b c.La composición se denota por
, si y son relaciones.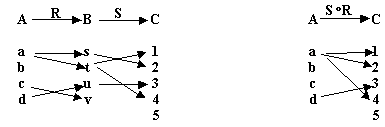
Bibliográfica Para Mas Información:
Dominio y Rango de una Relación
No hay comentarios:
Publicar un comentario