HOLA SOY HIKARI Y TE DOY LA BIENVENIDA A MI PÁGINA DE BLOG DE ÁLGEBRA!!
EN ESTE SITIO VAS A ENCONTRAR TODA LA INFORMACIÓN NECESARIA PARA LA UNIDAD#5
Matriz Booleana
Una matriz es un arreglo rectangular de números dispuestos en m reglones horizontales y n columnas verticales, cuyos elementos son 0 y 1 .Es por esto que se dice que las matrices booleanas tienen un orden de mxn.
Matriz de operaciones booleanas
Las operaciones que se pueden realizar entre matrices booleanas son tres: unión, conjunción y producto booleano. Estas operaciones no pueden realizarse sobre dos matrices cualesquiera, sino que deben cumplir ciertos criterios para poder llevarse a cabo. En particular, en el caso de la unión y la conjunción, las matrices que intervienen en la operación deben tener el mismo tamaño, y en el caso del producto booleano, las matrices deben cumplir con las mismas condiciones que para formar el producto de matrices.
Unión / Disyunción
Intersección / Conjunción
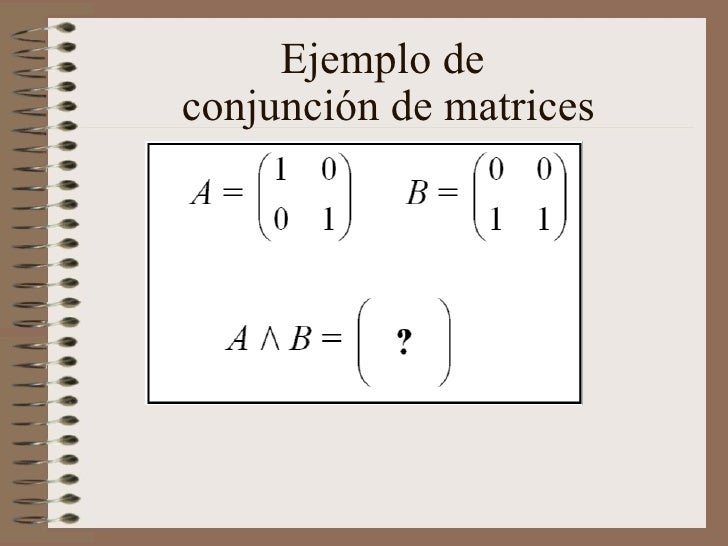
Producto booleano:
El producto booleano de las matrices A=[aij] y B=[bij], órdenes mxk y kxn respectivamente, se denotado por A O B. Este producto es la matriz mxn cuyo elemento (i,j ) es cij, donde:
Otras operaciones matriciales
La traspuesta de una matriz booleana es también otra matriz booleana; pero las operaciones con matrices booleanas no siempre producen matrices booleanas.
Matriz booleana asociada a una relación
Ejemplos:
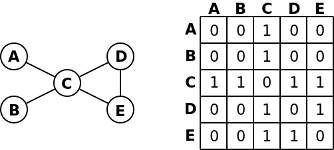
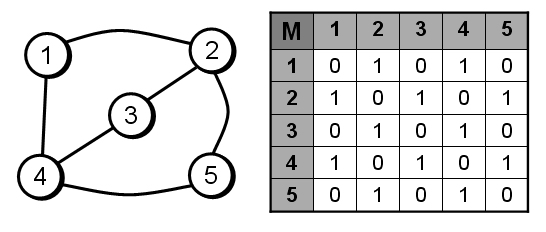
El grafo no-dirigido de la figura adjunta puede entenderse como una relación binaria. Dos elementos están relacionados si existe una línea que los una directamente. La matriz asociada a la relación binaria de conexión directa se llama matriz de incidencia, que es una matriz booleana que viene dada por:
El elemento ij de la anterior matriz es 1 si existe una línea que una directamente los círculos i y j y 0 en caso contrario
El grafo no-dirigido de la figura adjunta puede entenderse como una relación binaria. Dos elementos están relacionados si existe una línea que los una directamente. La matriz asociada a la relación binaria de conexión directa se llama matriz de incidencia, que es una matriz booleana que viene dada por:
Puerta lógica
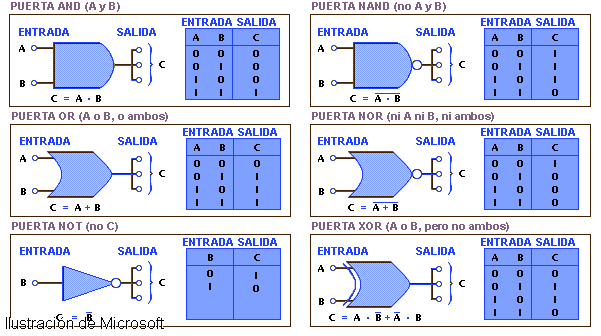
Una puerta lógica, o compuerta lógica, es un dispositivo electrónico con una función booleana. Suman, multiplican, niegan o afirman, incluyen o excluyen según sus propiedades lógicas. Se pueden aplicar a tecnología electrónica, eléctrica, mecánica, hidráulica y neumática. Son circuitos de conmutación integrados en un chip.experimentaba con relés o interruptores electromagnéticos para conseguir las condiciones de cada compuerta lógica, por ejemplo, para la función booleana Y (AND) colocaba interruptores en circuito serie, ya que con uno solo de éstos que tuviera la condición «abierto», la salida de la compuerta Y sería = 0, mientras que para la implementación de una compuerta O (OR), la conexión de los interruptores tiene una configuración en circuito paralelo.
Lógica Directa
Una puerta lógica, o compuerta lógica, es un dispositivo electrónico con una función booleana. Suman, multiplican, niegan o afirman, incluyen o excluyen según sus propiedades lógicas. Se pueden aplicar a tecnología electrónica, eléctrica, mecánica, hidráulica y neumática. Son circuitos de conmutación integrados en un chip.experimentaba con relés o interruptores electromagnéticos para conseguir las condiciones de cada compuerta lógica, por ejemplo, para la función booleana Y (AND) colocaba interruptores en circuito serie, ya que con uno solo de éstos que tuviera la condición «abierto», la salida de la compuerta Y sería = 0, mientras que para la implementación de una compuerta O (OR), la conexión de los interruptores tiene una configuración en circuito paralelo.
Lógica Directa
Puerta SÍ o BUFFER
La puerta lógica SÍ, realiza la función booleana igualdad. En la práctica se suele utilizar como amplificador de corriente o como seguidor de tensión, para adaptar impedancias (buffer en inglés).
La ecuación característica que describe el comportamiento de la puerta SÍ es:
Su tabla de verdad es la siguiente:
Tabla de verdad puerta Entrada Salida
La puerta lógica SÍ, realiza la función booleana igualdad. En la práctica se suele utilizar como amplificador de corriente o como seguidor de tensión, para adaptar impedancias (buffer en inglés).
La ecuación característica que describe el comportamiento de la puerta SÍ es:
Su tabla de verdad es la siguiente:
Tabla de verdad puerta Entrada Salida
Salida Puerta AND
La puerta lógica Y, más conocida por su nombre en inglés AND. (), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
La ecuación característica que describe el comportamiento de la puerta AND es:
La puerta lógica Y, más conocida por su nombre en inglés AND. (), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
La ecuación característica que describe el comportamiento de la puerta AND es:
Puerta OR
La puerta lógica O, más conocida por su nombre en inglés OR (), realiza la operación de suma lógica.
La ecuación característica que describe el comportamiento de la puerta OR es:
Su tabla de verdad es la siguiente:
La puerta lógica O, más conocida por su nombre en inglés OR (), realiza la operación de suma lógica.
), realiza la operación de suma lógica.
La ecuación característica que describe el comportamiento de la puerta OR es:
Su tabla de verdad es la siguiente:
Puerta OR-exclusiva (XOR)
La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es (signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en electrónica.
la puerta lógica XOR se identifica como función impar.
La ecuación característica que describe el comportamiento de la puerta XOR es:
Su tabla de verdad es la siguiente:
Puerta NOR-exclusiva (XNOR)
La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es (signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en electrónica.
(signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en
la puerta lógica XOR se identifica como función impar.
La ecuación característica que describe el comportamiento de la puerta XOR es:
Su tabla de verdad es la siguiente:
Puerta NOR-exclusiva (XNOR)
La puerta NOR exclusive, Conocida por su referencia en inglés XNOR, es el complemento de la puerta OR exclusiva, siendo su función booleana AB + A’B’. Se utiliza el mismo símbolo que la puerta OR exclusiva (signo más “+” inscrito en un círculo) y su representación en el diseño de circuitos lógicos y ecuación que la describe.
La puerta lógica XNOR se identifica como función par.
o también como:
Las tablas de verdad para dos y tres entradas o variables son las siguientes:
Tabla de verdad Puerta XNOR 2 Entradas
Entrada Entrada
0
0
1
0 1 0 1 0 0 1 1 1
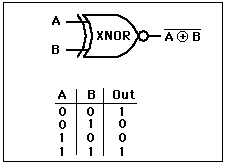
La puerta NOR exclusive, Conocida por su referencia en inglés XNOR, es el complemento de la puerta OR exclusiva, siendo su función booleana AB + A’B’. Se utiliza el mismo símbolo que la puerta OR exclusiva (signo más “+” inscrito en un círculo) y su representación en el diseño de circuitos lógicos y ecuación que la describe.
La puerta lógica XNOR se identifica como función par.
o también como:
o también como: 
Las tablas de verdad para dos y tres entradas o variables son las siguientes:
| Entrada | Entrada | |
|---|---|---|
0
|
0
|
1
|
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
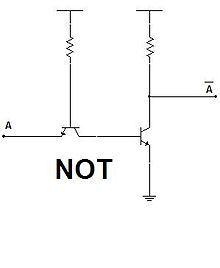
Puerta NO (NOT)
La puerta lógica NO (NOT en inglés) realiza la función booleana de inversión o negación de una variable lógica. Una variable lógica (A) a la cual se le aplica la negación se pronuncia como "no A" o "A negada".
La ecuación característica que describe el comportamiento de la puerta NOT es:
Su tabla de verdad es la siguiente:
La puerta lógica NO (NOT en inglés) realiza la función booleana de inversión o negación de una variable lógica. Una variable lógica (A) a la cual se le aplica la negación se pronuncia como "no A" o "A negada".
La ecuación característica que describe el comportamiento de la puerta NOT es:
Su tabla de verdad es la siguiente:
Mapa de Karnaugh
Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación defunciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2Nfilas, el mapa K correspondiente debe poseer también 2N cuadrados.
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadrícula de 4 × 4.
La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas. Por ejemplo, la celda en la esquina superior izquierda del mapa es 0, porque el resultado de la función es ƒ = 0 cuando A = 0, B = 0, C = 0, D = 0. De igual manera, la esquina inferior derecha es 10 porque el resultado de la función es ƒ = 10 cuando A = 1, B = 0, C = 1, D = 0.
Cubrir todos los unos del mapa mediante rectángulos de 2N elementos, donde N = 0 ... número de variables. Ninguno de esos rectángulos debe contener ningún cero (tal y como indicábamos en el apartado anterior).
§ Para minimizar el número de términos resultantes se hará el mínimo número posible de rectángulos que cubran todos los unos.
§ Para minimizar el número de variables se hará cada rectángulo tan grande como sea posible.
Véase que en este caso se ha unido la columna izquierda con la derecha para formar un único rectángulo.
Aplicaciones
Los diagramas de Karnaugh pueden ser utilizados en la simplificación de sentencias definidas en lógica Booleana, construcción de estaciones de clasificación, selección y control de calidad de piezas fabricadas, entre otras aplicaciones
Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación defunciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2Nfilas, el mapa K correspondiente debe poseer también 2N cuadrados.
Las variables de entrada pueden combinarse de 16 formas diferentes, por lo que el mapa de Karnaugh tendrá 16 celdas, distribuidas en una cuadrícula de 4 × 4.
La combinación de dígitos binarios en el mapa representa el resultado de la función por cada combinación de entradas. Por ejemplo, la celda en la esquina superior izquierda del mapa es 0, porque el resultado de la función es ƒ = 0 cuando A = 0, B = 0, C = 0, D = 0. De igual manera, la esquina inferior derecha es 10 porque el resultado de la función es ƒ = 10 cuando A = 1, B = 0, C = 1, D = 0.
Cubrir todos los unos del mapa mediante rectángulos de 2N elementos, donde N = 0 ... número de variables. Ninguno de esos rectángulos debe contener ningún cero (tal y como indicábamos en el apartado anterior).
§ Para minimizar el número de términos resultantes se hará el mínimo número posible de rectángulos que cubran todos los unos.
§ Para minimizar el número de variables se hará cada rectángulo tan grande como sea posible.
Véase que en este caso se ha unido la columna izquierda con la derecha para formar un único rectángulo.
Aplicaciones
Los diagramas de Karnaugh pueden ser utilizados en la simplificación de sentencias definidas en lógica Booleana, construcción de estaciones de clasificación, selección y control de calidad de piezas fabricadas, entre otras aplicaciones
ENLACE REFERENTE A LA UNIDAD:
VIDEO REFERENTES A ESTA UNIDAD
ENLACE REFERENTE A LA UNIDAD:
VIDEO REFERENTES A ESTA UNIDAD
No hay comentarios:
Publicar un comentario